Оптимальні LDPC матриці для виявлення помилок в квантових бітах у системах QKD
Основний зміст сторінки статті
Анотація
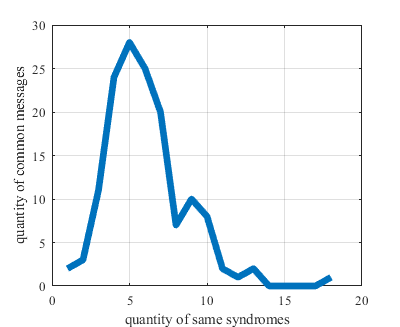
В даній роботі проаналізовано матриці перевірки на парність, які можуть бути використані в методі виправлення помилок на основі low density parity check (LDPC) матриць в системах квантового розподілу ключів. Система квантового розподілу ключів має неминучі помилки в просіяному ключі, які повинні бути виправлені алгоритмом виправлення помилок для створення захищеного ключа. У цьому аналізі 1000-бітні просіяні ключі розділяються на 50 частин, по 20 біт в кожній частині. Алгоритм створює 50 синдромів, по 10 біт в синдромі, що відповідають кожній частині, за допомогою перемноження матриць перевірки на парність розміром 10 × 20. Матриці перевірки на парність створюються алгоритмом, запропонованим Девідом Маккеєм та Редфордом Нілом. Процес створення синдрому складається з матричного перемноження 20-бітної частини просіяного ключа на матрицю перевірки на парність. Алгоритм посилає сформований синдром другій стороні. Під час передачі підслуховувач може перехопити синдром, але він не може дізнатись точне повідомлення з синдрому, навіть якщо він володіє матрицею перевірки на парність теж. Друга сторона також ділить її просіяний ключ на 50 частин, створює синдром з кожної частини і порівнює з отриманим синдромом. Якщо синдроми різні, ці частини просіяних ключів відкидають. Однак, через те, що довжина повідомлень складає 20 біт, а довжина синдромів 10 біт, можуть виникати ситуації, коли різні частини просіяного ключа матимуть однакові синдроми. Для даного випадку кожні 1024 повідомлень будуть мати один спільний синдром. Тому необхідно знайти таку оптимальну матрицю, яка знімає ймовірність отримання однакових синдромів від різних частин просіяного ключа.
Блок інформації про статтю

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Автори, які публікуються у цьому журналі, погоджуються з наступними умовами:- Автори залишають за собою право на авторство своєї роботи та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons Attribution License, котра дозволяє іншим особам вільно розповсюджувати опубліковану роботу з обов'язковим посиланням на авторів оригінальної роботи та першу публікацію роботи у цьому журналі.
- Автори мають право укладати самостійні додаткові угоди щодо неексклюзивного розповсюдження роботи у тому вигляді, в якому вона була опублікована цим журналом (наприклад, розміщувати роботу в електронному сховищі установи або публікувати у складі монографії), за умови збереження посилання на першу публікацію роботи у цьому журналі.
- Політика журналу дозволяє і заохочує розміщення авторами в мережі Інтернет (наприклад, у сховищах установ або на особистих веб-сайтах) рукопису роботи, як до подання цього рукопису до редакції, так і під час його редакційного опрацювання, оскільки це сприяє виникненню продуктивної наукової дискусії та позитивно позначається на оперативності та динаміці цитування опублікованої роботи (див. The Effect of Open Access).
Посилання
S. Wiesner, “Conjugate coding,” ACM SIGACT News, vol. 15, no. 1, pp. 78–88, Jan. 1983, DOI:10.1145/1008908.1008920.
R. L. Rivest, A. Shamir, and L. Adleman, “A method for obtaining digital signatures and public-key cryptosystems,” Commun. ACM, vol. 21, no. 2, pp. 120–126, Feb. 1978, DOI: 10.1145/359340.359342.
C. H. Bennett and G. Brassard, “BB84highest.pdf,” Proceedings of IEEE International Conference on Computers, Systems and Signal Processing. pp. 174–179, 1984.
P. Sibson et al., “Chip-based quantum key distribution,” Nat. Commun., vol. 8, no. May 2016, 2017, DOI: 10.1038/ncomms13984.
M. Lucamarini, Z. L. Yuan, J. F. Dynes, and A. J. Shields, “Overcoming the rate–distance limit of quantum key distribution without quantum repeaters,” Nature, vol. 557, no. 7705, pp. 400–403, May 2018, DOI: 10.1038/s41586-018-0066-6.
Z. Yuan et al., “10-Mb/s Quantum Key Distribution,” J. Light. Technol., vol. 36, no. 16, pp. 3427–3433, 2018, DOI: 10.1109/JLT.2018.2843136.
H.-K. Lo, M. Curty, and B. Qi, “Measurement-Device-Independent Quantum Key Distribution,” Phys. Rev. Lett., vol. 108, no. 13, p. 130503, Mar. 2012, DOI: 10.1103/PhysRevLett.108.130503.
C. H. Park et al., “Practical plug-and-play measurement-device-independent quantum key distribution with polarization division multiplexing,” IEEE Access, vol. 6, pp. 58587–58593, 2018, DOI: 10.1109/ACCESS.2018.2874028.
B. K. Park, M. K. Woo, Y.-S. Kim, Y.-W. Cho, S. Moon, and S.-W. Han, “User-independent optical path length compensation scheme with sub-nanosecond timing resolution for a 1 × N quantum key distribution network system,” Photonics Res., vol. 8, no. 3, p. 296, Mar. 2020, DOI: 10.1364/PRJ.377101.
T. A. Eriksson et al., “Crosstalk Impact on Continuous Variable Quantum Key Distribution in Multicore Fiber Transmission,” IEEE Photonics Technol. Lett., vol. 31, no. 6, pp. 467–470, 2019, DOI: 10.1109/LPT.2019.2898458.
G. Brassard and L. Salvail, “Secret-key reconciliation by public discussion,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 765 LNCS, pp. 410–423, 1994, DOI: 10.1007/3-540-48285-7_35.
W. T. Buttler, S. K. Lamoreaux, J. R. Torgerson, G. H. Nickel, C. H. Donahue, and C. G. Peterson, “Fast, efficient error reconciliation for quantum cryptography,” Phys. Rev. A - At. Mol. Opt. Phys., vol. 67, no. 5, p. 8, 2003, DOI: 10.1103/PhysRevA.67.052303.
Gallager, “Low density parity check codes,” 1963.
D. J. C. Mackay and R. M. Neal, “Good codes based on very sparse matrices,” in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 1995, vol. 1025, pp. 100–111, DOI: 10.1007/3-540-60693-9_13.
D. J. C. MacKay, “Good error-correcting codes based on very sparse matrices,” IEEE Trans. Inf. Theory, vol. 45, no. 2, pp. 399–431, 1999, DOI: 10.1109/18.748992.
N. Walenta et al., “A fast and versatile quantum key distribution system with hardware key distillation and wavelength multiplexing,” New J. Phys., vol. 16, 2014, DOI: 10.1088/1367-2630/16/1/013047.
W. C. Huffman and V. Pless, Fundamentals of Error-Correcting Codes. Cambridge University Press, 2003.
Radford M. Neal, “Software for Low Density Parity Check Codes.” 2012.